I'm going to try to break down the password algorithm from Castlevania 3 properly. If I can't fully comprehend it by the time I'm done with this post, I will apologize for wasting your time. But I don't think this will be a complete waste of time. Please note I am working "in reverse", analyzing the decryption algorithm first before tackling the encryption algorithm, as I feel the former provides some clarity to the latter.
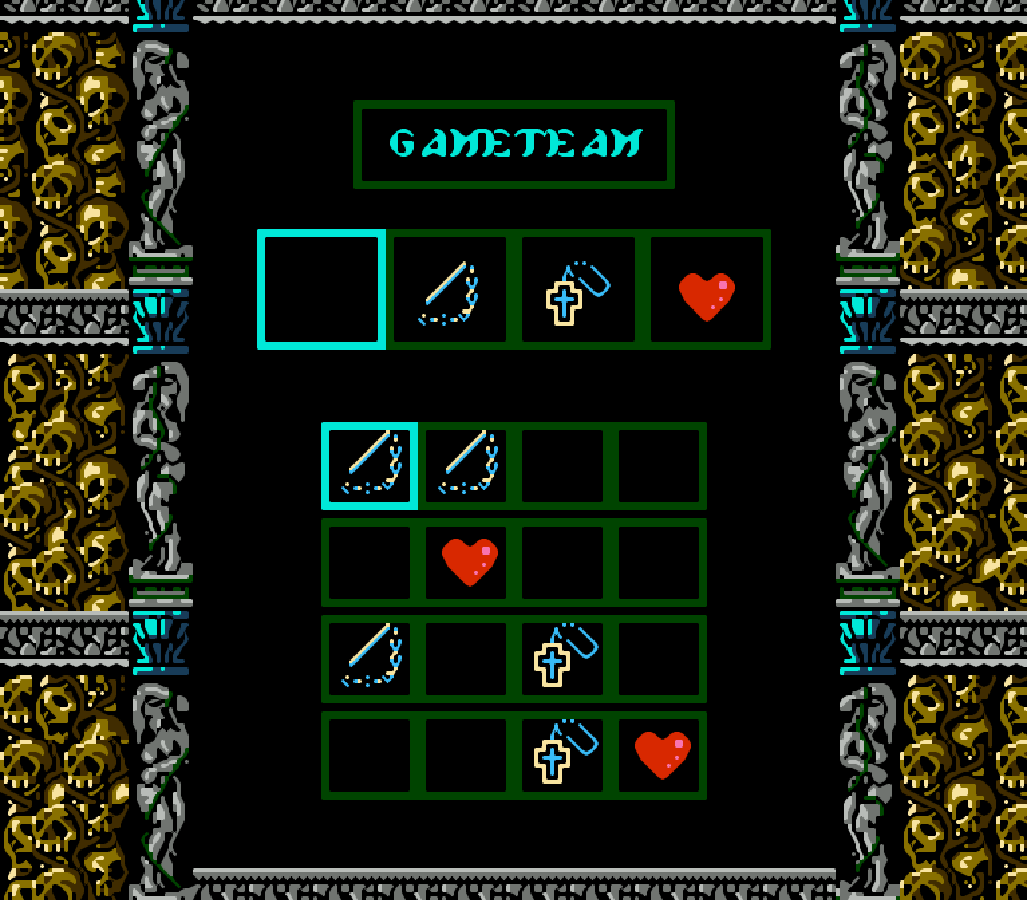
The password screen is laid out as follows (values are in hexadecimal):
Each place in the name will add its corresponding value to the letter assigned to that slot, as defined at addresses $7921 thru $7928 in CV3j. Technically you don't need to follow Castlevania III's lettering convention ('A' = 0x50) if you wanted to adopt this algorithm for your own projects outside of CV3. The name's total value is the sum of all modified letters modulo 8. Thus we see that 'A' in slot 0 has the same value as 'E' in slot 1 and as 'G' in slot 2 (0x50+0x07 ≡ 0x54+0x03 ≡ 0x56+0x01).
The unencrypted password consists of 16 bytes, all initialized to 0, with each cell in the password corresponding directly to a byte. The value of an icon placed in the cell is added to the base value of that cell and then saved to the corresponding byte. Although each cell has a base value as seen in the diagram above, the value is saved to a byte only when the icon value is greater than 0. In other words, if cell 1 (0x04) has no icon in it, then byte 1 will be 0x00, but if cell 1 has icon 2 in it, then byte 1 will be 0x06.
With that refresher out of the way, moving on....
Cells 0, 6 and 13 are reserved for the stage, hard-coded directly (meaning the lower bit is the column, the upper bit is the row, and modifying these should be reasonably safe) at addresses $7A1A thru $7A1C in CV3j. Every two stages have a reserved password value, hard-coded discretely at addresses $7B72 thru $7B7A in CV3j. When we map out each of these values, we see that each corresponds to either cell 0, 6 or 13. We can easily verify this using cv3pwgen to generate multiple passwords for one stage. All passwords will have at least one icon in common based on the stage selected.
- 0x01 = 0 whip
- 0x1B = 6 heart
- 0x02 = 0 cross
- 0x35 = 13 whip
- 0x19 = 6 whip
- 0x03 = 0 heart
- 0x37 = 13 heart
- 0x1A = 6 cross
- 0x36 = 13 cross
Since there are 18 stages (9 pairs) divvied up between 3 cells, all three icons get used. It follows thusly if the three reserved cells are changed, the discrete
stage values would need to be changed as well such that they coincide. I bring this up because it's an important facet of the algorithm. If we can understand the algorithm properly, we can change not only which cells are reserved for each stage, we can also increase the number of cells to coincide with additional stages.
The decryption algorithm loops through that array of values to find out which stage was set. It does this for all three cells, counting how many of them were set. If not one and only one cell is set, the algorithm will throw an error. In other words, amongst cells 0, 6 and 13, exactly one of them must have an icon placed in it.
Each of the three stage-reserved cells has 8 associated cells. If any cell set in the password is not an associated cell, the algorithm will throw an error. These associated cells are hard-coded directly at $78ED thru $7907 in CV3j. Including the stage-reserved cell, there are 9 cells total in each set. Consequently, the encrypted password is 9 bytes long. This is the same password the game generates when the player loses his last life.
The algorithm then takes all the lowest bits of each byte except the stage-reserved one and dumps them into one variable, then takes all the next lowest bits and dumps them into another variable (e.g., 0x3D21000005000000 would yield 0x13 and 0x00 respectively). The first variable is a checksum and the second variable contains all the real data.
As you can see, the randomizer and name take up a lot of valuable real estate. The randomizer alone, which is arguably pointless considering how so much of the algorithm is hard-coded, could be used instead for one additional stat, or two additional difficulty levels, or as four additional allies or ally combos. That's what you can get from just that single bit. The name takes up three bits -- that's 28 more allies! 😵 I'm getting carried away...
Anyway, if the name bits in that variable do not match the lowest 3 bits of the name entered by the player, the algorithm throws an error, naturally. The algorithm will also verify that the decrypted ally has access to the decrypted stage, unless using one of the special names in the US version.
After the algorithm finishes redefining each of the stats, the algorithm finally validates the checksum-hash. I call it a checksum-hash because it is very much a hash function, but is treated somewhat like a checksum. To do this, it treats the other variable as two distinct nybbles (4bit data), flips the odd bits (or even bits if randomized), then adds all the values together and checks if they hold up against the checksum. If it fails, then one of the stats might actually be wrong, so the algorithm will error out the entire password. I trust that this step is necessary, but it feels to me like it might only be relevant with the randomizer.
That's the decryption breakdown, to the best of my knowledge. That may have been a tad confusing at parts (I'm probably mostly to blame for that), but once you understand it, the encryption makes a bit more sense, since it is essentially just working the decryption algorithm in reverse sans most of the hashing.
First, you generate the AAAXYBBC variable. Then you generate your randomizer. With the randomizer chosen, you generate the checksum. Again, that's 0x50 (or 0xA0 if randomized) differentiated from each nybble of the first variable then added to the sum of the nybbles. Now you simply alternate adding individual bits of each of the two variables into your password array.
The algorithm then takes the stage, divides it by 2 (remember, stages are paired and their parity is treated separately), then finds which cell is reserved for that pair of stages. It then uses that cell to determine which of the three sets of allowed cells to use. Finally, it goes through each of those cells and checks if either of the correpsonding bits between AAAXYBBC and the checksum were set, generating the actual password to use for displaying the icons on the next screen.
And there you have it, an explanation to the best of my current ability, of the password encryption and decryption algorithm as posted on CastlevaniaDungeon.net's forums.
No comments:
Post a Comment